Anwendung der Hubbert´schen Peak-Oil-Theorie auf Gold
12.05.2010 | Dr. Jürgen Müller
 I. Einleitung
I. EinleitungDr. Marion King Hubbert (1903-1989) war ein amerikanischer Geologe, der von 1943 bis 1964 für Shell arbeitete und in dieser Zeit seine Peak-Oil-Theorie entwickelte. Diese besagt auf einen Nenner gebracht, dass sich die Produktionskurve von Öl in Form einer Glockenkurve entwickelt. Im Grunde müsste diese Theorie längst "Peak-Wahrheit" genannt werden, da Hubberts Vorhersagen eindrucksvoll durch die Realität bestätigt wurden. Fakt ist, dass sich keine Produktionskurve einer endlichen natürlichen Ressource immer weiter steigern läßt oder unbegrenzt lange auf einem hohen Niveau verharren kann. An einem bestimmten Punkt lassen Geologie und Technik keine weitere Produktionsausweitung mehr zu und es kommt nach einem Peak oder einem Plateau wieder zu einem Abfall der Fördermengen [1].
Unsere Erde ist ein endlicher Raum mit zwingend endlichen Ressourcen. Immer wieder kommt es an diesem Punkt zumeist zwischen Ökonomen und Ingenieuren/Geologen zum Streit. Erstere bemühen immer wieder das Grundprinzip von Angebot und Nachfrage und argumentieren, dass höhere Preise (d.h. größere Nachfrage) auch die Förderung wieder anheben würden. Sicherlich gilt dies für Güter des produzierenden Gewerbes. Leider gibt es im Bereich Ressourcenförderung jedoch viele Beispiele aus der Vergangenheit, die diese ökonomische Argumentation widerlegen, z.B. die Goldförderung des einstigen Hauptförderlandes Südafrika [2]. Obwohl der Goldpreis seit 1971 nicht mehr statisch an den Dollar gebunden war und bekannterweise bis 1980 ein dediziertes Peak bildete, ging die Förderung in Südafrika nach einem Peak im Jahr 1970 in dieser Zeit beständig nach unten, d.h. höhere Preise bewirkten explizit keine höhere Förderung. Auch die aktuelle Vervierfachung des Goldpreises in Dollar, verbunden mit einem Verfall des Randwertes, vermochte es nicht, diesen dramatischen Sinkflug zu stoppen.
In diesem Artikel soll in einem ersten Schritt die Hubbert-Theorie erläutert und nachfolgend auf die Goldförderkurve angewendet werden. Hubbert selbst betonte in seinen Schriften immer wieder, dass seine Mathematik auch auf mineralische Rohstoffe (sprich Metalle) anwendbar ist.
II. Bestimmung der kumulierten Gesamtfördermenge Q∞
Die Hubbert"sche Mathematik ist im Grunde recht simpel und beruht auf der Logistischen Funktion, die der belgische Mathematiker Verhulst 1838 zur theoretischen Beschreibung des Bevölkerungswachstumes entwickelt hatte [3]. Bevölkerungsentwicklung und Ölförderung hängen insofern logisch zusammen, als dass beide Wachstumskurven linear von den freien, noch zur Verfügung stehenden Kapazitäten abhängen. Im ersten Fall von der freien Kapazität der Erde, noch weitere Menschen zu ernähren und im letzteren Fall von dem Teil des Öls, welches noch "frei" zur Förderung in der Erde verblieben ist. Gehen die freien Kapazitäten zur Neige, sinkt auch die Geburten- bzw. Förderrate. Ein bildlicher Vergleich: Bei einer Ketchup-Flasche kommt zu Beginn das Ketchup oftmals wie ein Schwall geschossen, während man die letzten Tropfen mühsam herausschütteln- und klopfen muss. Nicht anders verhält es sich bei der bergbaulichen Gewinnung jedwelcher endlichen natürlichen Ressource.
Erster Kernpunkt der Theorie ist die Bestimmung der kumulierten historischen Fördermenge, d.h. der Menge, die in der Vergangenheit bereits gefördert wurde, plus der Menge die in der Zunkunft vermutlich noch gefördert werden wird. Geologen nennen diese Menge "Q" von (ausgesprochen) "qumulative". Die jährliche Produktionsrate einer Ressource wird mit "P" bezeichnet (für Produktion). Ohne an dieser Stelle auf die Herleitung der zugrunde liegenden Mathematik einzugehen [4]: Trägt man das Verhältnis von P zu Q in Prozent in Abhängigkeit von Q auf, so erhält man eine Kurve, die am Beginn des Produktionszykluses stark variiert, in ihrem weiteren Verlauf jedoch eine Gerade bildet, die man in die Zukunft verlängern kann und damit die zu erwartende Gesamtfördermenge Q∞ (Q unendlich) ermitteln kann. Abbildung 1 zeigt diese sog. "Hubbert-Linearisierung" für die bisherige globale Goldförderkurve.
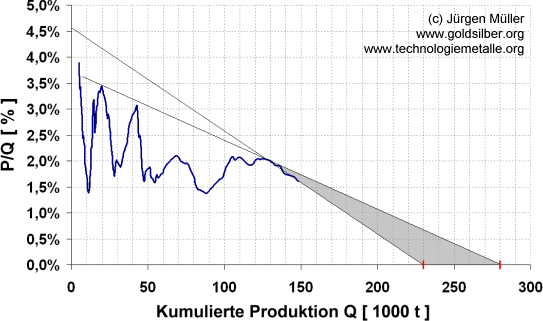
Abbildung 1: Hubbert-Linearisierung für Gold und sinnvolle Extrapolationen in die Zukunft [5]