Exkurs: Die Coronavirus-Verbreitung folgt keinem "exponentiellen Wachstum"
05.12.2021 | Prof. Dr. Thorsten Polleit
 Das Bundesverfassungsgericht hat am 30. November 2021 entschieden, dass der politisch diktierte Lockdown, die sogenannte »Bundesnotbremse«, verfassungskonform gewesen sei. Die obersten Richter schrieben u. a. in ihrer Urteilsverkündung:
Das Bundesverfassungsgericht hat am 30. November 2021 entschieden, dass der politisch diktierte Lockdown, die sogenannte »Bundesnotbremse«, verfassungskonform gewesen sei. Die obersten Richter schrieben u. a. in ihrer Urteilsverkündung:"Oberstes Ziel war es, die weitere Verbreitung des Virus zu verlangsamen sowie deren exponentielles Wachstum zu durchbrechen, um eine Überlastung des Gesundheitssystems insgesamt zu vermeiden und die medizinische Versorgung bundesweit sicherzustellen."
Die Richter sprechen von einem "exponentiellem Wachstum" bei der Ausbreitung des Coronavirus, und das macht den Leser doch sehr stutzig: Diese Worte offenbart eine grobe Fehleinschätzung. Um das zu erkennen, ist ein kurzer Blick in die mathematische Funktionslehre an dieser Stelle hilfreich.
Da gibt es zunächst die Potenzfunktion wie zum Beispiel in der Form: y = x². Hier steht die Veränderliche (die Variable) x in der Basis; y ist die Abhängige. Bei der Exponentialfunktion steht die Variable im Exponenten, also beispielsweise in der Form: y = 2x. Die nachstehende Graphik zeigt beispielhaft die Verläufe der Potential- und Exponentialfunktion.
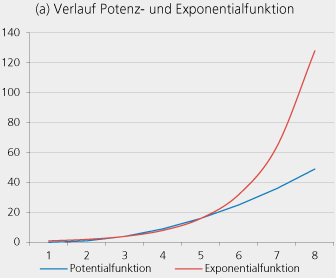
Quelle: Eigene Berechnungen.
Doch ist es sinnvoll beziehungsweise angemessen, das Infektionsgeschehen des Coronavirus als "exponentielles Wachstum" zu bezeichnen? In der Biologie und Medizin werden häufig zur Beschreibung von Prozessen sogenannte logistische Funktionen verwendet. Ein Anwendungsfall ist die Verbreitung von Infektionskrankheiten, bei der anschließend die Menschen eine permanente Immunität entwickeln, also im Zeitablauf eine abnehmende Anzahl von Personen übrig ist, die für die Infektionskrankheit anfällig bleibt. Diese Funktionen weisen (idealtypisch) einen S-förmigen Verlauf auf. Ein dafür Beispiel ist die Sigmoid-Funktion. Sie ist nachstehend abgebildet.

Quelle: Eigene Berechnungen. Gestrichelte Linie: Erste Ableitung der Sigmoid-Funktion.
Nehmen wir das Beispiel einer Infektionskrankheit. Anfänglich ist der Zuwachs der Infizierten/Erkrankten noch klein, nimmt dann zu und findet im Wendepunkt der Funktion seinen Höchststand, danach nimmt die Zuwachsrate wieder ab und steigt irgendwann gar nicht mehr. Sieht ein solcher Funktionsverlauf nicht viel weniger "bedrohlich" aus als der Verlauf einer "exponentiellen Funktion", die ja kein Ende zu nehmen scheint? Die Karlsruher Richter hätten ihre Worte umsichtiger wählen sollen; die Ausbreitung des Coronavirus folgt keinem exponentiellen Wachstumspfad.
© Prof. Dr. Thorsten Polleit
Auszug aus dem Marktreport der Degussa Goldhandel GmbH