Hubbert-Linearisierung für Gold
24.10.2017 | Dr. Jürgen Müller
 Die sogenannte "Hubbert-Linearisierung" (HL) zur Abschätzung der Gesamtfördermenge Q einer erschöpflichen Ressource wurde durch Hubbert selbst in seinem letzten Artikel aus dem Jahr 1982 in den Minen-Kontext eingeführt (Hubbert 1982) [1]. Dort wird auch die mathematische Herleitung des Prinzips aufgezeigt. Deffeyes, ein früherer Mitarbeiter von Hubbert bei Shell, merkte in seinem Buch "Beyond Oil" (Deffeyes 2006) [2] jedoch an, dass diese Methode schon einige Jahre zuvor von Biologen beschrieben und verwendet wurde (Smith 1963) [3].
Die sogenannte "Hubbert-Linearisierung" (HL) zur Abschätzung der Gesamtfördermenge Q einer erschöpflichen Ressource wurde durch Hubbert selbst in seinem letzten Artikel aus dem Jahr 1982 in den Minen-Kontext eingeführt (Hubbert 1982) [1]. Dort wird auch die mathematische Herleitung des Prinzips aufgezeigt. Deffeyes, ein früherer Mitarbeiter von Hubbert bei Shell, merkte in seinem Buch "Beyond Oil" (Deffeyes 2006) [2] jedoch an, dass diese Methode schon einige Jahre zuvor von Biologen beschrieben und verwendet wurde (Smith 1963) [3].Die grundsätzliche Vorgehensweise bei dieser Linearisierung ist wie folgt: Durch Auftragen des prozentualen Verhältnisses der jährlichen Förderung P zur bis dahin produzierten Gesamtförderung Q gegen Q, d. h. mathematisch ausgedrückt
P/Q [%] = f (Q) [Tonnen]
ist es für Produktionskurven, die einer logistischen Funktion folgen, möglich, durch die lineare Extrapolation zur Abszisse (x-Achse) die kumulierte Gesamtfördermenge Q∞, und durch Extrapolation zur Ordinate (y-Achse) den anfänglichen Wachstumsparameter "a" zu bestimmen, wobei letzterer von untergeordneter Bedeutung ist.
Wie in meinem letzten Artikel "Wieviel Gold?" dargestellt, wurden nach unseren Datenquellen bis 2016 kumuliert 175.187 Tonnen Gold gefördert. Die Jahresförderung im Jahr 2016 von 3.100 Tonnen entsprach demzufolge
P/Q₂₀₁₆ = 3.100 t / 175.187 t = 0,0177 = 1,77%
der bis dahin geförderten Gesamtmenge von Gold. Im Vorjahr 2015 betrug der Quotient noch
P/Q₂₀₁₅ = 3.100 t / 172.087 t = 0,0180 = 1,80%
d. h. der Prozentsatz verringert sich theoretisch im Laufe der Zeit, weil a) die Gesamtmenge Q im Nenner des Quotienten immer weiter steigt, und b) die jährliche Produktion P im Zähler des Quotienten irgendwann nach dem Peak-Gold Axiom zu sinken beginnt.
Im allgemeinen variiert das P/Q-Verhältnis in den frühen Jahren eines Produktionszyklus sehr stark, da selbst kleine Schwankungen in der Produktion zu großen Ausschlägen im prozentualen P/Q-Verhältnis führen können. Ist der Produktionszyklus jedoch hinreichend weit entwickelt, ergibt sich näherungsweise eine gerade Linie, die - in klassischer Interpretation - in die Zukunft extrapoliert werden kann. Der Schnittpunkt dieser Gerade mit der Abszisse ergibt den Erwartungswert für Q∞.
Am Beispiel der südafrikanischen Goldförderung, die bereits im Endstadium ist, kann das Prinzip sehr gut erkannt und erläutert werden.
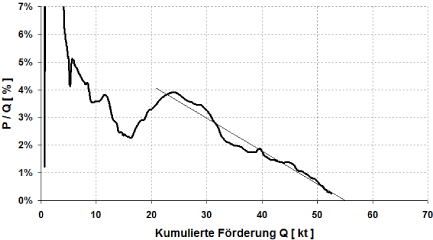
Abb. 1: Hubbert-Linearisierung der südafrikanischen Goldförderung
(Quelle: Eigene Berechnung und eigene Darstellung.)
(Quelle: Eigene Berechnung und eigene Darstellung.)
Im Jahr 1970 wurde mit 1.000 Tonnen das "Peak-Gold-Südafrika" erreicht. Im Jahr 2016 wurden nur noch 140 Tonnen gefördert. Da die Minenfelder im Witwatersrand um Johannesburg erst gegen Ende des 19. Jahrhunderts entdeckt wurden, ist die geschichtliche Förderung seit 1883 sehr gut dokumentiert. In Summe wurden in Südafrika bis einschließlich 2016 52.500 Tonnen Gold gefördert (d. h. ca. 30% der globalen Gesamtmenge von ca. 175 kt), sodass die Jahresförderung 2016 von 140 Tonnen nur noch einen Prozentsatz von 0,27% ausgemacht hat.
Der gesamte Förderzyklus nähert sich somit seinem Ende. In Abb. 1 ist zu erkennen, wie sich seit 1965 (bei P/Q = 3,9%) näherungsweise eine Gerade gebildet hat, die man durch einen mathematischen Fit gegen die Abszisse extrapolieren kann. Man kommt somit auf einen Erwartungswert für das südafrikanische Q∞ von ca. 55.000 Tonnen (Schnittpunkt der gefitteten Geraden mit der x-Achse). D. h. bis zum Ende der (groß-industriellen) Förderung werden noch ca. 2.500 Tonnen Gold in Südafrika förderbar sein.